Les méthodes formelles peuvent être utilisées pour donner une spécification du système que l'on souhaite développer, au niveau de détails désiré.

Une spécification formelle du système est basée sur un langage formel dont la sémantique est bien définie (contrairement à une spécification en langage naturel qui peut donner lieu à différentes interprétations). Cette description formelle du système peut être utilisée comme référence pendant le développement. De plus, elle peut être utilisée pour vérifier (formellement) que la réalisation finale du système (décrite dans un langage informatique dédié) respecte les attentes initiales (notamment en termes de fonctionnalité).

Une fois qu'une spécification a été développée, elle peut être utilisée comme référence pendant le développement du système concret (mise au point des algorithmes, réalisation en logiciel et/ou circuit électronique). Par exemple:

• Si la spécification formelle est dotée d'une sémantique opérationnelle, le comportement observé du système concret peut être comparé avec le comportement de la spécification (qui elle-même doit être exécutable ou simulable). De plus, une telle spécification peut faire l'objet d'une traduction automatique vers le langage cible.
• Si la spécification formelle est dotée d'une sémantique axiomatique, les préconditions et postconditions de la spécification peuvent devenir des assertions dans le code exécutable. Ces assertions peuvent être utilisées pour vérifier le fonctionnement correct du système pendant son exécution (ou simulation), ou mieux encore des méthodes statiques (preuve de théorème, model-checking) peuvent être utilisées pour vérifier que ces assertions seront satisfaites pour toute exécution du système.

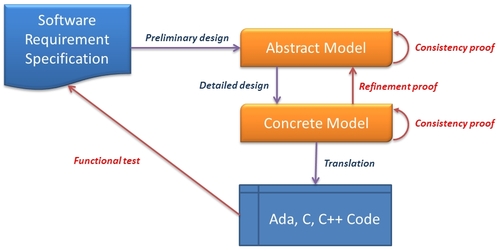
Une spécification peut être utilisée comme base pour prouver des propriétés sur le système. La spécification est le plus souvent une représentation abstraite (avec moins de détails) du système en développement: débarrassé de détails encombrants, il est en général plus simple de prouver des propriétés sur la spécification que directement sur la description complète et concrète du système.

Certaines méthodes, comme la Méthode B s'appuient sur ce principe: le système est modélisé à plusieurs niveaux d'abstraction, en partant du plus abstrait et en allant au plus concret (ce processus est appelé « raffinement » puisqu'il ajoute des détails au fur et à mesure); la méthodologie assure que toutes les propriétés prouvées sur les modèles abstraits sont conservées sur les modèles concrets. Cette garantie est apportée par un ensemble de preuves dites «de raffinement».

"C'est en essayant encore et encore que le singe apprend à bondir"

Voir aussi : http://urbanisation-si.blog4ever.net/

http://urbanisation-si.over-blog.com/

http://urbanisation-des-si.blogspot.fr/

http://urbanisation-si.eklablog.com/

http://rhonamaxwel.over-blog.com/